Haskellには種(kind)という仕組みがあります。大雑把に言ってしまえば、「型の型」を実現する仕組みです。この仕組みについて、あまり情報が出回っていないようなので、解説記事を残しておこうと思います。なお、前編と後編に分かれていて、この記事は後編になります。前編はこちらになります。
この記事は、Ladder of Functional Programming (日本語訳)の FIRE LUBLINE(ADVANCED BEGINNER) を対象に、Part 1の続きとして、種に付随するGHC言語拡張やパッケージを紹介するものです。
なお、特に断らない限り、対象としてGHC8系を設定しています。stackを使ってる方はresolverをLTS Haskell 7以降に設定しておくことを推奨します。
Link to
here様々な種
Link to
here型制約の種
前回の記事では、種の基本的な仕組みを紹介しました。全てのデータ型は*という種を持っており、データ宣言は*の種を持つ型を作る型コンストラクタを定義するのでした:
>>> newtype WrappedInt = WrappedInt Int
>>> :kind WrappedInt
WrappedInt :: *
>>> data Tag a = Tag
>>> :kind Tag
Tag :: * -> *さて、Haskell標準には上のようなデータ型を表す*と、型コンストラクタを表すk1 -> k2という形の種(例えば、* -> *や* -> (* -> *)など)しかありませんでした。GHCでは、他にもいくつか種を導入しています。今日は、その幾つかを紹介していきます。一つ目が、型制約を表す種Constraintです。この種を伴う仕組みはConstraintKinds拡張により導入できます。
Haskellの型上には、データ型や型コンストラクタの他にも、型制約という登場人物がいます。型制約は名前の通り、型の制約が書けるようにするものです。以下の関数をみてください:
minByOrd :: Ord a => a -> a -> a
minByOrd x y = if x < y then x else yこの関数minByOrdは、型aが順序を持つ(Ordクラスのインスタンスである)という制約を満たしている時、二つの引数のうち小さい方をOrdのメソッド<を使用して返します。
型制約は、型クラスを使うことで作ることができます。例えば、ある型がデフォルトの値を持つという制約は、以下のように書けます:
class HasDefault a where
defaultValue :: aこの型クラスを使うことで、デフォルトの値を持つ型制約を満たしている型上では、defaultValueメソッドを使用することができるようになります。例えば、以下のようにです:
fromMaybe :: HasDefault a => Maybe a -> a
fromMaybe (Just x) = x
fromMaybe Nothing = defaultValueこの関数は、型aがHasDefault aという型制約を満たしているならば、Maybe aの値をパターンマッチし、中身がJustならそのままJustを外して値を返し、Nothingならデフォルト値をdefaultValueメソッドを使用して、返します。
ここからが本題です。実はGHC上では、型制約にも種が割り当てられています。見てみましょう:
>>> :kind HasDefault
HasDefault :: * -> ConstraintHasDefault型クラスは、*の種を持つ型を受け取り、Constraintの種を持つ型制約を返します。ConstraintはGHCが導入している、型制約を表す種です。型制約は、GHC上ではこの 型制約種Constraint を持ちます。つまり、HasDefault :: * -> Constraintは、*の種の型、つまりデータ型を一つ受け取り、型制約になるような型上の関数になります。実際に、データ型を適用して型制約にしてみましょう:
>>> :kind HasDefault Bool
HasDefault Bool :: Constraint適用結果は、ちゃんとConstraintの種を持っています。ここで、種の計算では型の計算は行われないことに注意してください! kindコマンドは、型の計算は行わないのでした。私たちは、BoolをHasDefaultのインスタンスにしていないため、実際にはこの型制約は満たされません。型の計算を実際に行ってみましょう。上で定義したfromMaybeを実際にBool型に使ってみます:
>>> :type fromMaybe $ Just True
<interactive>:1:1: error:
• No instance for (HasDefault Bool)
arising from a use of ‘fromMaybe’
• In the expression: fromMaybe $ Just True「HasDefaultはBoolに対してインスタンスを持っていない」と型エラーになっていることが分かります。このように型の計算はtypeコマンドで確かめることができるのでした。これらの型計算は、もう少し直接的に確かめることもできます。次を見てください:
>>> :set -XFlexibleContexts
>>> :type undefined :: HasDefault Bool => Bool
<interactive>:1:1: error:
No instance for (HasDefault Bool) arising from a use of ‘it’このように、型の計算だけを行わせる場合、undefinedを使用するのが便利です。Haskell標準では、型制約はあまり柔軟には書けません。具体的な型を伴う上のような制約も書けないため、FlexibleContexts拡張を使用することで書けるようにしています。上の型表記で登場する、=>という表記は、左で指定された型制約を満たしているならば右で指定された型付けの関数になる、という意味を持っています。つまり、型上の演算子として考えるなら、(=>) :: Constraint -> * -> *という種になります。なので、例えば以下のような型表記は、種の辻褄が合わなくなります:
>>> :kind Int => Bool
<interactive>:1:1: error:
• Expected a constraint, but ‘Int’ has kind ‘*’
• In the type ‘Int => Bool’
>>> :kind HasDefault => Bool
<interactive>:1:1: error:
• Expecting one more argument to ‘HasDefault’
Expected a constraint, but ‘HasDefault’ has kind ‘* -> Constraint’
• In the type ‘HasDefault => Bool’kindコマンドによって、種が合わないとエラーになっていることが分かります。残念ながら、=>は実際には型演算子ではなく、(=>)というように型関数として扱うことはできません。ですが、それは表記上の問題であり、確かに種の計算の際、型制約を受け取る型演算子として、Constraintの種を持つか検査が行われていることは分かるでしょう。
さて、今までは型制約種Constraintについて、GHCi上で色々試しながら見てきました。型制約種に関しての雰囲気は分かってもらえたと思います。型制約種Constraintをもう少し詳しく見ていきましょう。以下を見てください:
>>> data SimpleData a = SimpleData a
>>> :kind SimpleData
SimpleData :: * -> *
>>> class SimpleClass a where simpleMethod :: a -> a
>>> :kind SimpleClass
SimpleClass :: * -> Constraintデータ宣言と型クラス宣言を並べてみました。この二つはよく似ています。
- データ宣言は、
*という種の型になるような型コンストラクタSimpleData :: * -> *を作り、SimpleData :: a -> SimpleData aという値コンストラクタを作ります。 - 型クラス宣言は、
Constraintという種の型制約になるようなSimpleClass :: * -> Constraintを作り、simpleMethod :: SimpleClass a => a -> aというような関数を作ります。
作られるものがそれぞれ違いますが、両方型の世界に一つの型関数、値の世界に関数を作るわけです。型クラスの方をデータ宣言に合わせるとしたら、型クラスは型制約コンストラクタとメソッドを作るものと言えるかもしれません。型の世界だけでの話なら、データ宣言は型コンストラクタを、型クラスは型制約コンストラクタを単に作るだけの構文ということになります。ではここで、データ型と型制約の対比を表にしてみましょう。
| 種 | 表現される型 | 定義方法 |
|---|---|---|
* |
データ型 | データ宣言(data C a = ...) |
Constraint |
型制約 | 型クラス宣言(class C a where ...) |
両者はそれぞれ特別な意味を与えられています。実際、データ型が値を持ち1、それによって型注釈が書けるように、型制約は=>という特別に型制約を計算するような型上の構文を持っています。ですが、逆に言えば特別なのはそれだけで、それ以外に両者の違いはありません。例えば、Proxy型は種多相化されているので、型制約や型制約コンストラクタ(型クラス)を渡すこともできます:
>>> import Data.Proxy
>>> :kind Proxy
Proxy :: k -> *
>>> :type Proxy :: Proxy (Monoid Bool)
Proxy :: Proxy (Monoid Bool) :: Proxy (Monoid Bool)
>>> :type Proxy :: Proxy Monoid
Proxy :: Proxy Monoid :: Proxy Monoid=>を使用していないので、型制約の計算は行われないことに注意してください! また、Proxy型コンストラクタは、それぞれ以下のように特殊化されます:
Proxy :: Proxy (Monoid Bool)の場合は、Proxy :: Constraint -> *Proxy :: Proxy Monoidの場合は、Proxy :: (* -> Constraint) -> *
では、このProxyで型制約を受け取り、型制約の計算だけを行うような関数を作って使って見ましょう。その関数は、以下のように作ることができます:
>>> :set -XConstraintKinds
>>> import Data.Proxy
>>> -- 型制約計算を行う関数を定義
>>> :{
evalConstraint :: a => Proxy a -> ()
evalConstraint _ = ()
:}
>>> -- この段階では、まだ型制約計算されない!
>>> Proxy :: Proxy (Monoid Bool)
Proxy
>>> -- 型制約計算をする関数に適用
>>> evalConstraint (Proxy :: Proxy (Monoid Bool))
<interactive>:12:1: error:
• No instance for (Monoid Bool)
arising from a use of ‘evalConstraint’
• In the expression: evalConstraint (Proxy :: Proxy (Monoid Bool))
In an equation for ‘it’:
it = evalConstraint (Proxy :: Proxy (Monoid Bool))
>>> evalConstraint (Proxy :: Proxy (Monoid String))
()やっと、ConstraintKinds拡張の登場です。ConstraintKinds拡張は、型制約に関するHaskell標準の制限を幾つか取り払う拡張です。どのようなことが可能になるかは後で紹介するとして、今は上の関数の使い方に注目しましょう。この例のように、型制約はProxy型で持ち回し=>で任意のタイミングで型制約計算を行うといったことも可能です。面白いですね。
上のProxyを使った例から明らかですが、もちろんデータ宣言時に種注釈を使うことで型制約を受け取るようなデータ型を作ることもできるわけです。そして、型制約を受け取るような型クラスも作ることができます。次の例を見てください:
>>> :set -XKindSignatures -XFlexibleInstances
>>> import GHC.Exts (Constraint)
>>> class AConstraint (c :: Constraint)
>>> :kind AConstraint
AConstraint :: Constraint -> Constraint
>>> instance AConstraint (Monad Maybe)FlexibleInstances拡張は、FlexibleContexts拡張と同じような拡張で、FlexibleContextsは型制約の書き方の制限を、FlexibleInstances拡張はインスタンスの書き方の制限をそれぞれ取り払う拡張です。また、Constraint種はGHC.Extsモジュールに入っていて、使用する際はこのモジュールをimportする必要があります。これらを使って、上のようにすれば、型制約の分類分けすらすることができるようになります。
他にもConstraintに関連する特殊な型上の演算子があります。普段気にも留めていなかったと思いますが、型制約のペアです。GHC上では、以下のような型制約が書けます:
>>> -- 常に型制約は満たされる
>>> :type undefined :: () => a
undefined :: () => a :: a
>>> -- 二つの型制約が満たされる場合に、満たされる
>>> :type undefined :: (Monad m, Monoid a) => m a
undefined :: (Monad m, Monoid a) => m a
:: (Monoid a, Monad m) => m a
>>> -- 以下の二つは同じ
>>> :set -XConstraintKinds
>>> :type undefined :: (Monad m, Monoid a, Show a) => m a
undefined :: (Monad m, Monoid a, Show a) => m a
:: (Show a, Monoid a, Monad m) => m a
>>> :type undefined :: ((Monad m, Monoid a), Show a) => m a
undefined :: ((Monad m, Monoid a), Show a) => m a
:: (Show a, Monoid a, Monad m) => m a最後の例ではConstraintKinds拡張を使用していますが、これについては最後にどんな拡張なのか説明しましょう。今、注目してもらいたいのは、型制約のペアについてです。普段何気なく使っていると思いますが、これらも一種の型制約の演算子と見ることができるわけです。注意してもらいたいのが、この演算子はタプル型と同じ形式だということです。次を見てください:
>>> :kind ()
() :: *
>>> :kind (Bool, Int)
(Bool, Int) :: *
>>> :kind (Monad Maybe, Monoid Bool)
(Monad Maybe, Monoid Bool) :: Constraint
>>> :kind (Bool, Monad Maybe)
<interactive>:1:8: error:
• Expected a type, but ‘Monad Maybe’ has kind ‘Constraint’
• In the type ‘(Bool, Monad Maybe)’
>>> :kind (Monad Maybe, Bool)
<interactive>:1:15: error:
• Expected a constraint, but ‘Bool’ has kind ‘*’
• In the type ‘(Monad Maybe, Bool)’()は、ユニット型の方が優先されています。(,)は、最初に書いた型の種によって、受け取る種が左右されていることが分かりますね。型制約のペアは、(,) (Monad Maybe) (Monoid Bool)というような表記は許容されていませんが、それ以外はあまりタプル型と変わりありません。異なるのは、タプル型が幾つかのデータ型を受け取って一つのデータ型となるのに対し、型制約のペアは型制約を幾つか受け取りそれを全て満たすような型制約になるということです。
最後にConstraintKinds拡張をきちんと紹介しておきましょう。ConstraintKinds拡張は、次のようなことを可能にしてくれる拡張です。
- 型エイリアスと同じ構文で、型制約コンストラクタのエイリアスを書くことができるようになる。
つまり、次のようなことが可能になります:
{-# LANGUAGE ConstraintKinds #-}
-- 型制約のエイリアス
type MonMonad m a = (Monoid (m a), Monad m)
-- 型制約コンストラクタのエイリアス
type Mappable = Functor- 型制約種
Constraintを持つ型を、型制約として使用できるようにする。
こちらは、あまり実感が湧かないかもしれません。デフォルトで、GHCでは型クラスなどを型制約として扱う、つまり=>に渡すことができます。ですが、Constraintの種を持つ型制約変数などを渡すことはできません:
>>> import Data.Proxy
>>> -- 型クラスを型制約として使っているため、問題ない
>>> :type undefined :: Monad m => m a
undefined :: Monad m => m a :: Monad m => m a
>>> -- 型制約変数は、型制約として扱えない
>>> :type undefined :: a => Proxy a
<interactive>:1:14: error:
• Illegal constraint: a (Use ConstraintKinds to permit this)
• In an expression type signature: a => Proxy a
In the expression: undefined :: a => Proxy a
>>> :set -XConstraintKinds
>>> -- 型制約種を持つものなら、型制約として扱えるようになる
>>> :type undefined :: a => Proxy a
undefined :: a => Proxy a :: a => Proxy a((Monad m, Monoid a), Show a)などが標準で扱えないのも、(Monad m, Monoid a)という形式のものは型制約種を持ってはいますが、標準で許容されている形式ではないからです。このような場合に、より柔軟に扱えるようにしてくれる拡張が、ConstraintKinds拡張です。
型制約種Constraintについて、馴染んでもらえたでしょうか?普段、この種やConstraintKindsを明示的に使うような場面は少ないかもしれませんね。もし、型制約種について興味を持ったなら、constraintsというパッケージを見てみるのが良いでしょう。このパッケージは、型制約プログラミングに関する幾つかの有用なAPIを提供しています。
Link to
hereデータ型の昇格
今までは、*やConstraint、k1 -> k2といった、予め用意された特別な種を紹介してきました。GHC上で、私たちが種を定義するような方法も、実は用意されています。それが、DataKindsという拡張です。DataKindsは基本的には簡単な拡張です。
私たちは、以下のようなデータ宣言を使ってデータ型を定義することができました:
data SimpleData a = SimpleData aこのデータ宣言は、
SimpleData :: * -> *な、SimpleData aというデータ型を作るような型コンストラクタSimpleData :: a -> SimpleData aな、SimpleData aというデータ型の値を作る値コンストラクタ
をそれぞれ作るのでした。DataKindsは、このそれぞれのコンストラクタを、一つ上の層に昇格させることができるようになる拡張です。どういうことかは、見てみた方が早いと思うので、GHCi上でいくつか試してみます:
>>> -- 単純なデータ型を作成
>>> data SimpleData a = SimpleData a
>>> -- DataKinds拡張有効化
>>> :set -XDataKinds
>>> -- 通常のコンストラクタ
>>> :kind SimpleData
SimpleData :: * -> *
>>> :type SimpleData
SimpleData :: a -> SimpleData a
>>> -- DataKindsによって、一つ上の層に昇格させたコンストラクタ
>>> :kind 'SimpleData
'SimpleData :: a -> SimpleData a最後の実行例に注目してください。ここで書かれているSimpleDataは値コンストラクタのものです。先頭に'(シングルクォーテーション)がついていますが、何より注目すべきなのは、種の表示にもやはりSimpleDataというものが現れていることです。これが一つ上の層に昇格させるということになります。DataKinds拡張は、以下のようなものを提供する拡張になります:
- データ型の型コンストラクタを、種上で書けるようにする(種への昇格)
- データ型の値コンストラクタを、先頭に
'を付けることにより型上で書けるようにする(型への昇格)
上の実行例では、'SimpleData :: a -> SimpleData aの、
- 種の表記に現れているものが、型コンストラクタ
SimpleData :: * -> *を昇格したもの 'SimpleDataが、値コンストラクタSimpleData :: a -> SimpleData aを昇格したもの
になります。値コンストラクタSimpleDataは型多相化されたコンストラクタなので、それを昇格させた'SimpleDataは種多相化された型コンストラクタになります。上の実行例の、
- 最初の
SimpleData :: a -> SimpleDataという表示でのaは、任意の(*という種を持つような)型を、 - 二つ目の
'SimpleData :: a -> SimpleData aのaは、任意の種を、
それぞれ表すということに注意してください。では、種多相化されていることを確認してみましょう。以下を見てください:
>>> :kind 'SimpleData Bool
'SimpleData Bool :: SimpleData *
>>> :kind 'SimpleData Maybe
'SimpleData Maybe :: SimpleData (* -> *)
>>> :kind 'SimpleData Monad
'SimpleData Monoid :: SimpleData (* -> Constraint)Proxy型のように、どんな値でもとれるようになっていることが分かると思います。注意して欲しいのは、値コンストラクタ、型コンストラクタがそれぞれ一つ上に昇格されたので、'SimpleData Monoidという型を持つような値は存在しないということです。値を作るコンストラクタは昇格して型コンストラクタになってしまいましたからね! 値を持つ型は全て、*という種を持つのでしたね。SimpleData aという種は*と一致しないため、値を持たないということもできます。値が存在しないならば、一体どういう場面で役に立つのでしょうか? 一つの活用例としては、データ型のタグに利用ができます。以下を見てください:
{-# LANGUAGE KindSignatures #-}
data GET
data POST
data PUT
data DELETE
data Request (a :: *) = Request String
forGetMethod :: Request GET -> ...この例は、HTTPのリクエストが、どんなメソッドでのリクエストかを、タグ情報で持つような例です。このタグ情報によって、処理を型安全に分けることができます。しかしながら、以下の問題点があります。
- 各メソッドのタグが別々のデータとして宣言されていて、集約されていません。
Request型も、メソッド用のタグの他にも*という種を持っているならどんな型でも、例えばRequest Boolといった型を作ることもできるようになってしまいます。
DataKindsを使うことで、もう少しタグ情報を明確に書くことができます。それは、以下のような修正をくわえることで、実現できます:
{-# LANGUAGE DataKinds, KindSignatures #-}
data HttpMethod
= GET
| POST
| PUT
| DELETE
data Request (a :: HttpMethod) = Request String
forGetMethod :: Request 'GET -> ...この例では、DataKinds拡張を使うことで、前の例での欠点を修正しています。メソッド情報はHttpMethodというデータ型の宣言に集約していますし、種に昇格させたデータ型で種注釈を行うことで、RequestはHttpMethod以外の型がとれないようになっています。このように、DataKindsは値を持ちませんが、タグを表す型としてとても便利です。
その他にも、DataKinds拡張は、シングルトンというものを定義することによって、より有用になる場合があります。ただし、これらの話は種の話題というよりは型レベルプログラミングの話題になるので、この記事では紹介しません。興味がある方は、singletonsという有用なパッケージがあるので、見てみると良いでしょう。
ところで、DataKindsは、リスト型[a]、タプル型(a, b)などにも適用できます。まずリスト型の昇格から見ていきましょう。以下を見てください:
>>> :set -XDataKinds -XTypeOperators
>>> :kind '[]
'[] :: [k]
>>> :kind '(:)
'(:) :: a -> [a] -> [a]
>>> :kind Functor ': Applicative ': Monad ': '[]
Functor ': Applicative ': Monad ': '[] :: [(* -> *) -> Constraint]
>>> :kind '[Functor, Applicative, Monad]
'[Functor, Applicative, Monad] :: [(* -> *) -> Constraint]リストの値コンストラクタは二つ、[] :: [a]、(:) :: a -> [a] -> [a]でした。また、リストは特別な構文として、[True, False] == True : False : [] :: [Bool]といったようなものが書けるのでした。これらをそれぞれ昇格させたものが上のものになります。タプル型の方は、以下のようになります:
>>> :kind '()
'() :: ()
>>> :kind '(,)
'(,) :: a -> b -> (a, b)
>>> :kind '(Bool, Monad Maybe)
'(Bool, Monad Maybe) :: (*, Constraint)
>>> :kind '(,,,)
'(,,,) :: a -> b -> c -> d -> (a, b, c, d)タプル型もリスト型と大体同じような感じですね。
さてここからは、DataKindsのもう少し詳細な見方を紹介しておきましょう。DataKindsは型コンストラクタを種上に昇格、値コンストラクタを型上に昇格させることをできるようにするような拡張でした。実は、Constraintやk1 -> k2という種も昇格された種とみなすことができます。
Costraintの方は単純で、以下のようになっています:
>>> import GHC.Exts (Constraint)
>>> :info Constraint
data Constraint -- Defined in ‘GHC.Types’見ての通り、GHC.Typesというモジュールで定義された、値コンストラクタを持たないデータ型です。この型がDataKindsと違うところは、
- デフォルトで、型コンストラクタ
Constraint :: *が、種に昇格可能なこと - 型制約は、
Constraint型が昇格された種に結び付けられること
だけで、他はDataKindsと同じです。なので、昇格前は単純に値も型引数も持たないデータ型です。見てみましょう:
>>> import GHC.Exts (Constraint)
>>> :kind Constraint
Constraint :: *確かにConstraintが、*を種に持つ型であることが分かりますね。
k1 -> k2の方はちょっと特殊で、関数型コンストラクタ(->)が昇格したものになっています。関数型は関数に結びついているデータ型でした。Constraintの時と同じように定義を見てみると、以下のようになっています:
>>> :info (->)
data (->) t1 t2 -- Defined in ‘GHC.Prim’
infixr 0 `(->)`
...関数型もやはり値コンストラクタを持ちません。ですが、Constraintと違い、関数型は関数という値を持ちます。Haskell上では、a -> bという型を持つ値は、a型の値を受け取りb型の値を返すような関数になるのでしたね。これらの関数を作る操作、例えばラムダ記法や関数宣言などが、関数型の値コンストラクタと言えるでしょう。これらがそれぞれ昇格すると、a -> bという種は、aの種を持つ型を受け取り、bの種を持つ型を返すような、型上の関数を表します。つまり、
a -> bという関数型を、種a -> bに昇格a -> bという型の関数を、a -> bという種の型関数に昇格
という感じの対応をすることになります。こう見ると、少々特殊ではありますが、DataKindsでの昇格したデータ型と同じような扱いと思うことができます。
このように、Constraintやk1 -> k2でさえ、DataKindsの昇格と同じように見ることができます。*はどうでしょうか?実は、*だけは少し特別です。見てみましょう:
>>> import GHC.Types
>>> :kind *
* :: *さて、GHC.Typesモジュールには、データ型*が定義されています。このデータ型は自身を、つまり*の昇格された種を持っていると見ることができます。つまり、次のような型表記も可能です:
>>> import GHC.Types
>>> :kind * -> *
* -> * :: *種においての* -> *とは、上の型が種に昇格されたものとなるわけです。もちろん、次のような型表記もできます:
>>> :set -XDataKinds
>>> import GHC.Types
>>> :kind * -> Constraint
* -> Constraint :: *
>>> :kind 'Just Int
'Just Int :: Maybe *
>>> :kind Maybe *
Maybe * :: *これらをもっと視覚的にまとめてみましょう。型が結びついている種は、どのような型が昇格したものかをまとめてみると、以下のようなグラフの形になるわけです:
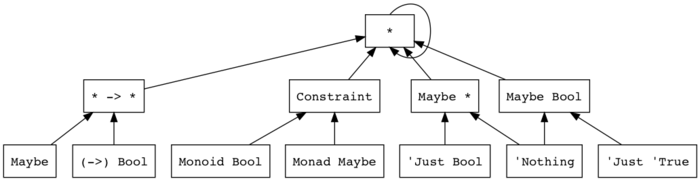
'Nothing :: Maybe aであることに注意してください。'Nothingは種多相化されているので、'Nothing :: Maybe *とすることも、'Nothing :: Maybe Boolとすることも可能です2。
このように見てみると、私たちが種と呼んでいたものは、単にある型に付属する単なる型情報だと思えてきます。種注釈とは、単にその型がどういう型に付属しているかの情報に過ぎないのです。そして、値にもやはり型情報が付属しています。値とDataKindsによって型に昇格したものを同一視してみると、値と型の間には差異はないということになりますね。このアイデアを元に、GHCでは TypeInType という拡張が提供されています。この拡張は後ほど紹介しましょう。
最後に名前空間の話をしておきましょう。全ての種は、ある型が昇格したものである、という話をしました。GHCでは、そういう背景があり、種の名前空間は型の名前空間と完全に一致します。ただし、値の名前空間と型の名前空間を完全に一致させることはできません。それはHaskellが多用している、型コンストラクタと値コンストラクタの名前を同じにするという文化があるからです。以下の例を見てください:
>>> :set -XDataKinds
>>> data A a = A a | B a
>>> :kind A
A :: * -> *
>>> :kind 'A
'A :: a -> A a
>>> :kind B
B :: a -> A aBの例は、'を書いていないのに型に昇格できていますね。DataKindsは値と型の名前で被るものが無いようなものは'を書かなくていいようになっています。これは型から種へ昇格できる時は自然な動作でしたが、値から型の場合、今回でいうAのように型コンストラクタと値コンストラクタの名前が被ってしまうケースが出てきます。もちろん、データ型Bが新しく宣言されてしまうような場合もあるでしょう。このように、型から種へは名前空間が一致しますが、値から型へは名前が被るのを避けるために'を付けるようにしているのです。なので、本質的には値から型へも、'を付けないで昇格させることが理想です。それを覚えておきながら、DataKinds拡張使用の際は、'を適切に付けていくのが良いでしょう。
Link to
here型の分類
最後に、少し変わった型と、それにまつわる種の分類分けについてお話ししましょう。この見方は、よりGHCのプリミティブな部分に携わる時に、役にたつはずです。Haskell標準では、種は*とk1 -> k2しかありませんでした。GHCでは、それに型制約種Constraintが追加されてるのでしたね。そして、DataKinds拡張を使えば、データ型を種に昇格することもできました。しかし、結局値を持つ型は*という種を持つのでしたね。ですが、この制約には一部例外があります。それは、GHCのプリミティブな値についてです。
私たちは普段何気なくInt型やDouble型を使用しています。しかしながら、これらは実際に実行するとき、メモリ上でどのような構造で保持されているのか考えたことはないでしょうか? ここでは詳細な話はしませんが、幾つか基本的なGHCでの内部表現についてお話ししましょう。GHCiで、この二つの型の情報を表示してみましょう。
>>> import Prelude (Int, Double)
>>> :info Int
data Int = GHC.Types.I# GHC.Prim.Int# -- Defined in ‘GHC.Types’
>>> :info Double
data Double = GHC.Types.D# GHC.Prim.Double#
-- Defined in ‘GHC.Types’どうやらこの二つの型は、不思議な値コンストラクタを持っているようですね。
Intデータ型は、一つの値コンストラクタI# :: Int# -> Intを持ちます。Doubleデータ型は、一つの値コンストラクタD# :: Double# -> Doubleを持ちます。
Int#やDouble#といった見慣れないデータ型が出てきましたね。これらが今回紹介するGHCの用意しているプリミティブなデータ型です。せっかくですから、上の値コンストラクタを使って、それぞれのデータ型の値を作ってみましょう。それにはMagicHash拡張が必要です。通常、#のついた値や型は、私たちは扱うことができません。それを可能にするのがMagicHash拡張です。また、IntやDoubleの値は、1といった数値リテラルで作れるのでした。同じように、Int#やDouble#といった不思議なデータ型にも、それぞれのリテラルが用意されています。使ってみましょう:
>>> :set -XMagicHash
>>> import GHC.Types (Int(..), Double(..))
>>> -- I#を使って、Int型を作る
>>> :type 1#
1# :: GHC.Prim.Int#
>>> I# 1#
1
>>> :type I# 1#
I# 1# :: Int
>>> -- D#を使って、Double型を作る
>>> :type 1.0##
1.0## :: GHC.Prim.Double#
>>> D# 1.0##
1.0
>>> :type D# 1.0##
D# 1.0## :: Double各リテラル表記は、次のようになっています:
Int#のリテラルは、整数と#で作ることができます。Double#のリテラルは、実数と##で作ることができます。
他にも幾つか#の付くデータ型があるのですが、まずはこのデータ型がどのようなものなのかについて、紹介しましょう。これらのデータ型は、 プリミティブ型(primitive types) と呼ばれます。そして、その多くが 非ボックス型(unboxed types) と呼ばれています。
GHCでは、多くのデータ型はボックス化、つまりヒープ上に参照データとして格納されています。データ型の値自体はポインタで、本体はヒープ上にあるというわけです。これは、データ型が、値コンストラクタを複数持つ場合もありますし、複数の様々なデータ型を取るパラメータを持つこともあり、サイズが多岐に渡るからです。しかし、ヒープに格納するには、格納する場所を計算して領域を確保し、必要なくなったら領域を解放しなければならないという、大きなコストがかかります。これは、サイズが大きなデータ型については、いちいち領域をコピーし実データのまま扱うよりも、低コストになる場合が多いですが、サイズが固定されていて尚且つ小さなデータの場合、大きな足かせになります。このため、GHCは幾つかの特別なデータ型を用意し、そのデータ型はヒープ上に格納せず直接実データとして扱うようにしています。それが、非ボックス型です。
また、GHCは非ボックス型の他にも幾つか特別なデータ型を用意しています。Array#やMutableArray#、MVar#などのデータ型です。これらは、実データとしてではなくヒープ上に格納され、ポインタをデータとするようなものです。つまり、ボックス化されているわけです。しかしながら、通常のデータ型と異なり、ヒープ上のデータは特殊な構造をしています。このように、GHCが用意している、Haskell上では定義できない特殊な構造を持つデータ型をボックス化されている/されていないに関わらず、プリミティブ型と言います。少し、まとめておきましょう:
- プリミティブ型とは、GHCが事前に用意している、Haskellの構文では定義できない、値が特殊な構造を持つようなデータ型のこと。
- 非ボックス型とは、ボックス化されていない型、つまりポインタとして表現されるのではなく実データとして表現されるような値を持つ型のこと。
さて、この記事は種についての記事なので、種の話もしましょう。プリミティブ型は、GHCでは*ではなくそれぞれが特別な種を割り当てられています。見てみましょう:
>>> :set -XMagicHash
>>> import GHC.Prim (Int#, Double#)
>>> :kind Int#
Int# :: TYPE 'GHC.Types.IntRep
>>> :kind Double#
Double# :: TYPE 'GHC.Types.DoubleRepなにやら、不思議な種が登場しました。一体これらの種は、どのようなものなのでしょうか? infoコマンドで見てみましょう:
>>> import GHC.Types
>>> :info TYPE
data TYPE (a :: RuntimeRep)
-- Defined in ‘GHC.Prim’
>>> :info RuntimeRep
data RuntimeRep
= VecRep VecCount VecElem
| TupleRep [RuntimeRep]
| SumRep [RuntimeRep]
| LiftedRep
| UnliftedRep
| IntRep
| WordRep
| Int64Rep
| Word64Rep
| AddrRep
| FloatRep
| DoubleRep
-- Defined in ‘GHC.Types’注記: この実行例はGHC 8.2.1のものですが、これらのデータ型は現在かなりアグレッシブな変更が加えられており、表現方法がバージョンによってかなり異なります。ただし、データ型の意味は特に変わらないはずなので、手元の環境の実行例に差異があっても、特に気にしないでください!
TYPE :: RuntimeRep -> *、RuntimeRep :: *、共に特に難しい定義ではありませんね。RuntimeRepは”runtime representation”(実行環境での表現)という意味を表した名前になっています。前の章でのデータ型の昇格の話を思い出してください。TYPE 'IntRepという種は、TYPE 'IntRepという型が昇格したものになります。'IntRepは、RuntimeRepデータ型の値コンストラクタIntRepが、型に昇格したものということを思い出してください。つまり、値IntRepを型に昇格した'IntRepが、さらに種に昇格しているということになります。ちゃんと型が合ってるかは、昇格される前の型で調べれば良いのですね。いちよGHCiで確認してみましょう:
>>> import GHC.Types
>>> :kind TYPE
TYPE :: RuntimeRep -> *
>>> :kind 'IntRep
'IntRep :: RuntimeRep
>>> :kind TYPE 'IntRep
TYPE 'IntRep :: *ちゃんと種が符合していることが分かりますね。RuntimeRepやTYPEは、*やConstraint、a -> bなどと同じく、DataKinds無しで特別に種に昇格することが許可されています。この特別なデータ型によって、プリミティブ型は表現されています。幾つかのプリミティブ型に対する対応を、表にしてみました:
| プリミティブ型 | 非ボックス型か? | 紐づいている種 | リテラル | C言語での型表現 |
|---|---|---|---|---|
Char# |
o | TYPE 'WordRep |
文字と#('x'#) |
int32_t |
Int# |
o | TYPE 'IntRep |
整数と#(3#) |
int |
Word# |
o | TYPE 'WordRep |
整数と##(3##) |
unsigned int |
Float# |
o | TYPE 'FloatRep |
実数と#(3.2#) |
float |
Double# |
o | TYPE 'DoubleRep |
実数と##(3.2##) |
double |
Addr# |
o | TYPE 'AddrRep |
文字列と#("foo"#) |
void * |
Array# a |
x | TYPE 'UnliftedRep |
- | - |
MutableArray# s a |
x | TYPE 'UnliftedRep |
- | - |
MVar# s a |
x | TYPE 'UnliftedRep |
- | - |
この他にもGHCはプリミティブ型を用意しています。プリミティブ型は、ghc-primパッケージのGHC.Primモジュールにて公開されています。興味があれば、種を確認しながら見てみると面白いでしょう3。また、TupleRepやSumRepを持つ型は、それぞれUnboxedTuples拡張、UnboxedSums拡張を使用する必要があります。こちらについても、気になる方は調べてみてください。
さて、プリミティブ型は、その表現方法によって種が用意されていることは分かったと思います。最後に、このRuntimeRepの中で二つの特殊な要素LiftedRepとUnliftedRepについて話しておきましょう。データ型を表す種として、*を紹介しました。実はこの種は、次のようなエイリアスになっています4:
type * = TYPE 'LiftedRepつまり、今まで見てきたデータ型は、実行時にliftedという枠組みで表現されるようなものというわけです。では、このliftedとunliftedの違いはなんなのでしょうか? それの説明に入る前に、GHCにおいての評価戦略とデータの内部表現についての話をしておきましょう。ときに、Haskellは遅延評価デフォルトの言語です。例えば、以下の式の評価は例外になりません:
>>> f :: Int -> Int; f _ = 0
>>> f (error "raise an exception")
0GHCでは、このようなerror "raise an exception"という式は評価されるまでは実際の値でなく、サンクという計算式を表現したデータとして保持されます。サンクは一度評価されると破棄され、実際の値にすげ変わります。上の関数fが受け取るのは、このサンクまたはすげ変わった実際の値を指し示すようなポインタです。今回の場合、error "raise an exception"という、まだ評価されていない式のサンクを指し示すポインタというわけです。上の例では、関数fに渡されたサンクを示すポインタは、特に評価されないまま捨てられ、定数値が返ってきます。では、サンクを評価するような関数を作って、動かしてみましょう:
>>> f :: Bool -> Int; f b = if b then 0 else 1
>>> f (error "raise an exception")
*** Exception: raise an exception
CallStack (from HasCallStack):
error, called at <interactive>:2:4 in interactive:Ghci2この例では先ほどと違い、受け取ったサンクを関数fの中のif文で評価しています。そのため、例外が発生しているわけです。サンクはGHCが遅延評価を実装するための仕組みであり、lifted型の値は指し示す先がサンクになり得るようなポインタで表現されます。lifted型とは、その値としてボトムと称される値になるようなものも持てるような型のことです。ボトムと呼ばれる値には、主に以下のようなものがあります:
- 評価すると例外が出されるような値
- 無限ループになっていて永遠に評価が終わらないような値
Haskellの通常の型は、上のような式を表すサンクをも値として持ちますから、無限ループになったり例外が出されたりするような値、つまりボトムをも表現できます。それに対して、GHCではボトムを表現できない型も存在します。その典型が非ボックス型です。非ボックス型はポインタではなく、実データとして表されているんでしたよね。実データは、サンクとすげ替えるということができないですよね。では、非ボックス型を処理するような関数に、undefinedを渡すとどうなるか、見てみましょう:
>>> :set -XMagicHash
>>> import GHC.Exts
>>> f :: Int# -> Int; f _ = 0
>>> f (error "raise an exception")
*** Exception: raise an exception
CallStack (from HasCallStack):
error, called at <interactive>:7:4 in interactive:Ghci4先ほどのliftedの例(Intの例)と、何が違うか分かりますか? 今回、関数fはやはり受け取った値を無視して定数を返します。どこにも受け取った引数を評価する箇所はありません。
- liftedの例(
Intの例)では、undefinedを評価せず、つまり例外が一切出ずに定数が返ってきました。 - 今回の非ボックス型の例(
Int#の例)では、例外が発生しています。
なぜでしょうか? 実は、非ボックス型は遅延評価ではなく正格評価が行われます。その理由はお分かりですね? なぜなら遅延評価のためにサンクを用意しようにも、非ボックス型はサンクを表現できないからです! 非ボックス型として値を格納するならば、サンクではなく評価した後の実データでないといけません。そのため、ボックス型の引数を受け取る関数の場合は、一旦引数に渡される式を評価して実データにした上で、関数に渡すということを行います。実は、これは非ボックス型だけに止まりません。GHCでは、ボックス型の中にも正格評価になるような、つまりサンクを値として持たないような型があります。それが、TYPE 'UnliftedRepを種に持つデータ型です。見てみましょう:
>>> :set -XMagicHash
>>> import GHC.Exts
>>> f :: Array# a -> Int; f _ = 0
>>> f (error "raise an exception")
*** Exception: raise an exception
CallStack (from HasCallStack):
error, called at <interactive>:8:4 in interactive:Ghci2Array# aはヒープ上に本体があり、それを指し示すポインタで表現されます。ただしこのポインタは、サンクを指し示すことはありません。つまりかならず実データを指し示すことになり、ボトムを値に持つことはないのです。
ところで、今までは引数がunliftedな型である場合の話をしてきましたが、返り値がunliftedな型になっている場合はどう見ることができるのでしょう?例えば、次のような関数を考えてみてください:
{-# LANGUAGE MagicHash #-}
import GHC.Exts
infLoop :: Int# -> Int#
infLoop i = infLoop (i +# 1#)(+#) :: Int# -> Int# -> Int#は、GHCで用意されているInt#専用の加算演算子です。この関数は問題なく定義することができますが、実行すると無限ループを起こします。つまりinfLoop 1# :: Int#というような式はボトムを表しているように見えます。unliftedな型は、ボトムを持たないはずでは無かったのでしょうか? 注意して欲しいのは、infLoop 1#という式は、それ単体ではHaskellでは単なる表記に過ぎないということです。この式は、なんらかのトップレベル関数や定数の一部になっているはずです。関数はliftedな型の値です(関数型は、a -> b :: *であることを思い出してください!)。関数はコンパイルされ、ランタイムによって実行されます。つまり、最終的に実行時に意味を持つのは、トップレベルの関数であり、それはliftedな型で表現されるということです。また、Haskellではunlifted型のトップレベル定数の宣言は許されていません。以下のコードはコンパイルエラーになります:
{-# LANGUAGE MagicHash #-}
import GHC.Exts
-- 許可されていない
unliftedConstant :: Int#
unliftedConstant = 1#これにより、トップレベルの関数や定数は、全てliftedな型を持つことになります。もし、内部でunliftedな式が無限ループや例外を吐くなら、それはその式を含んだトップレベルのliftedな関数や定数が、ボトムを表すサンクを持つことになるということです。これは、unliftedの考え方を逸脱しません。
- トップレベルの関数や定数はサンクを持つliftedな値に翻訳され、
- unliftedな型を持つ引数は、受け取る前に正格に評価され、サンクを持たない値となった後関数に渡されます。
このような解釈によって、Haskellでのlifted/unliftedの枠組みは保たれます。
ボトムについての形式的な議論は、領域理論という分野でされています。もし、lifted/unliftedについての理論的な背景が知りたいなら、領域理論や表示的意味論について学習してみると良いでしょう5。
ここまでのことを大雑把にまとめておきました。GHCでは型について幾つかの大別をしています:
- プリミティブ型/非プリミティブ型: GHCが自前で用意している特殊な型か、Haskellで定義可能な型か
- ボックス型/非ボックス型: ポインタで表され本体はヒープにあるような参照型か、実データで表される型か
- lifted型/unlifted型: サンクを持ちボトムを値として含むような型か、サンクを持たない型か
なお、非ボックス型はunliftedであり、liftedな型はボックス型になります6。では、幾つかの型の種別を見て、今回は終わりにしましょう(type * = TYPE 'LiftedRepであることに注意してください!):
| 型名 | 種 | プリミティブ型か | ボックス型か | liftedか |
|---|---|---|---|---|
Bool |
TYPE 'LiftedRep |
x | o | o |
Int# |
TYPE 'IntRep |
o | x | x |
Array# a |
TYPE 'UnliftedRep |
o | o | x |
Link to
hereこの章のまとめ
この章では、型制約を表す種Constraintの紹介、型を種に、値を型に昇格するDataKinds拡張の紹介、そしてプリミティブ型の種とGHCの型の大別について、お話ししました。
型制約には型制約種Constraintという種がつくのでした。データ宣言が型コンストラクタと値コンストラクタを作るように、型クラスは型制約コンストラクタと型制約下でのメソッド群を作るものとみることができました。また、型制約は、=>によって制約が満たされるか検査されるのでしたね。ただ、Haskell標準では型制約は決まった形状でしか書けませんでした。そのため、ConstraintKinds拡張が用意されており、この拡張によって型制約種を持つものならば変数であろうと型制約のペアであろうと、型制約として扱えるようになるのでした。また、この拡張によって、型制約のエイリアスも書けるようになりました。
DataKindsはデータ型の型コンストラクタを種において使えるように、値コンストラクタを型において使えるようにするものでした。値コンストラクタは、昇格の際先頭に'をつけるのでした。また、Haskellの種全般が、何かしらの型が昇格したものとみなせるという話もしましたね。*ですら、一つのデータ型でした。
最後に、GHCのプリミティブ型、ボックス型、lifted型という大別を紹介しました。
- プリミティブ型は、Haskellでは定義できないGHCが事前に用意してくれている型でした。例えば
Int#、Array#などがそうです。 - ボックス型の値は、ポインタで表現されヒープ上に本体を持ちました。非ボックス型の値は、実データとして表現されます。
- lifted型の値は、評価されるまではサンクを指すポインタとなっており、
undefinedなどの評価すると例外になるようなものや無限ループでさえ値として持ち得るのでした。unlifted型の値は、サンクを持たず、正格に評価されるのでした。
以降では、少し高度な種に関する話題を紹介していきます。あまり知られてない機能や最近入った機能、まだ入ってない提案中のものなども紹介していきます。これらの話題は、最初に掲げた想定読者層から外れているのであまり詳しくは紹介しません。こんな話もあるんだぐらいに留めておいてもらえれば、良いでしょう。
Link to
hereAdvanced Topics
Link to
hereもう一つの型の分類
今までは、種に関する基本的な話題を紹介しました。ここでは、種とは別の、もう一つの型に付属する種別情報を紹介しましょう。それは、type roleと呼ばれるものです。type roleは、GeneralizedNewtypeDerivingという拡張と、密接な関係があります。
ここでは詳しく解説しませんが、GeneralizedNewtypeDerivingという拡張は、newtypeで作った型のクラスインスタンス導出を簡略化するための拡張で、そのインスタンスを元の型のものを持ってきて実装します。この拡張は利便性を向上させますが、その導出が壊れるケースが出てきます。例えば次のケースです:
{-# LANGUAGE GeneralizedNewtypeDeriving, StandaloneDeriving, TypeFamilies #-}
newtype Age = MkAge { unAge :: Int }
type family Inspect x
type instance Inspect Age = Int
type instance Inspect Int = Bool
class BadIdea a where
bad :: a -> Inspect a
instance BadIdea Int where
bad = (> 0)
deriving instance BadIdea Age -- 壊れた導出になる
{- | 上のものは、以下のものと同じ
instance BadIdea Age where
bad = coerce (bad :: Int -> Inspect Int)
-}Age -> Inspect AgeはAge -> Intと同じ、Int -> Inspect IntはInt -> Boolと同じであるということに注意してください。この場合、AgeとIntは同じ実行時表現を持ちますが、IntとBoolは同じ表現を持たないわけですから、直感的にはInt -> Inspect IntをAge -> Inspect Ageにキャストすることは型の健全性を壊します。
type roleは、二つの型が同じ表現を持つ型かどうかを判断するために、組み込まれた機能です。つまり、キャストが型安全にできるかを判断するためのものなのです。データ型や型クラス、型族などの型変数は、type roleを持ちます。type roleの概念は、aとbという型が同じ表現を持つときに(例えば、IntとAgeは同じ表現を持ちます)、型コンストラクタや型族Tに対してT aとT bが同じ表現を持つかを判断するための機構で、Tのどのパラメータが判断するときに関与するか、という情報を持ちます。type roleは以下の三種類があります:
nominal: 受け取ったパラメータの型が例え同じ表現であっても、全体として同じ表現になるとは限らないことを示します:
type family F a -- a has nominal type role data D a = D (F a) -- a has nominal type rolerepresentational: 受け取ったパラメータの型が同じ表現であるならば、全体としても同じ表現になることを示します。一般的にはこのtype roleを持ちます:
data Simple a = Simple a -- a has representational type rolephantom: 受け取ったパラメータが、表現に全く関与しないことを示します:
data Tag a = Tag -- a has phantom type role
これらのtype roleは推論によって決定するようになっているため、私たちは普段特に意識する必要はありません。ただし、推論結果が意図しないものである場合もあります。その際は、RoleAnnotations拡張を使って、以下のようにすることで、type roleを明示的に書くこともできます:
type role T nominal _ phantom
data T a b c = T Int b_は推論に任せることを意味します。
type roleに興味があるならば、GHC User’s Guide - 9.36 Rolesを読んでみると良いでしょう。また、歴史的経緯については、Roles: a new feature of GHCに簡潔にまとまっています。
Link to
here軽率多相
前の章では、プリミティブ型の種を紹介しました。この種はTYPE :: RuntimeRep -> *という型コンストラクタを昇格したものによって、作られているのでした。そして、*でさえTYPE 'LiftedRepのエイリアスでしか無かったのでしたね。このような種の表現になったのは、実は最近のことです。昔はそれぞれの種は実行時の表現ごとに切り離されていました。TYPEを使って共通化されたのには、幾つかの歴史的経緯があり、 軽率多相(levity polymorphism) という話題と密接な関係があります。軽率多相は、種多相を少し制限したものです。種多相は任意の種を扱えるような種変数を許容しますが、軽率多相は実行時表現に関係するような範囲での種の多相を提供します。
関数型コンストラクタ(->)の種は、(->) :: * -> * -> *であると話してきました。実際には、(->) :: TYPE q -> TYPE r -> *というような種を持っています。TYPEの引数の部分は、任意のRuntimeRepをとれるようになっています。確認してみましょう:
>>> :set -XTypeInType -XKindSignatures
>>> import GHC.Exts
>>> type CheckFuncType (q :: RuntimeRep) (r :: RuntimeRep) (a :: TYPE q) (b :: TYPE r) = a -> b -- no errorTypeInType拡張については、後ほど解説しますので、今はおまじないとしておきましょう。上の例では、任意のRuntimeRepに対して、確かに関数型コンストラクタが有効であることが確認できます。このように関数型コンストラタは軽率多相化されています。なので、私たちはInt# -> Int#といったような関数を、通常の関数型の表記で書けるようになっていたのです。
関数型が軽率多相化されているということは、軽率多相化された関数が書けるということでもあります。実際、幾つかの関数は軽率多相化された形で提供されています。例えば($)やerrorなどがそうです。ただし、軽率多相は全てに気軽に適用できるというわけではありません。以下の例を考えて見ましょう:
{-# LANGUAGE TypeInType, KindSignatures, ExplicitForAll #-}
import GHC.Exts (RuntimeRep, TYPE)
bad :: forall (r1 :: RuntimeRep) (r2 :: RuntimeRep)
(a :: TYPE r1) (b :: TYPE r2).
(a -> b) -> a -> b
bad f x = f xこの例は、($)を軽率多相化した例になります。しかし、この実装には幾つかの問題があります。badをコンパイルすることを考えてみてください。badの引数fはただの関数なので問題ありませんが、引数xは軽率多相化されています。xは果たして実データかポインタかどちらでしょうか? また、サンクを持っているのでしょうか? xのビット幅は? xはどのレジスタに格納すべきでしょうか? 私たちはコンパイル時に、この質問に答えることはできません。なぜなら実データである場合もありポインタである場合もありますし、サンクを持っているかもしれません。浮動小数点数である場合も整数である場合もあり、ビット幅も一定ではないからです! つまり私たちは、badの引数xをどのように扱えばいいのか、コンパイル時に決めることができないのです。これは、引数が軽率多相化された関数全てに対して当てはまることです。このため、GHCでは軽率多相化したような変数を使った関数宣言は許可されていません。ですが、注意して欲しいのは、次のような関数は作ることができるということです:
{-# LANGUAGE TypeInType, KindSignatures, ExplicitForAll #-}
import GHC.Exts (RuntimeRep, TYPE)
good :: forall (r1 :: RuntimeRep) (r2 :: RuntimeRep)
(a :: TYPE r1) (b :: TYPE r2).
(a -> b) -> a -> b
good f = fこの場合、軽率多相化された変数はどこにも出てきていません。
ところで、軽率多相の焦点は、実行時表現の中でもlifted/unliftedの枠組みについてです。liftedな型の値はサンクを持ち遅延評価を主とし、unliftedな型の値はサンクを持たないので正格評価になるのでしたね。このサンクを持つ持たないに関わらず関数を多相化して書けるようにするのが、軽率多相の主な目的です。ですが、GHCではもう一つ重要なboxed/unboxedという枠組みもあるのでしたね。この二つの枠組みを分けて多相化できるように、現在次のような変更も提案されています:
data Boxity = Boxed | Unboxed
data Levity = Lifted | Unlifted
data TYPE (b :: Boxity) (l :: Levity)
type * = TYPE 'Boxed 'Liftedもし、軽率多相に興味があるならば、原論文Levity Polymorphism (extended version)を読んでみるのがいいでしょう。この論文では、軽率多相に至るまでのGHCでの経緯と問題点、軽率多相の動機などが丁寧に解説されています。また、論文より説明が若干劣りますがGHC User’s Guide - 9.12 Levity polymorphismにも、GHCでの軽率多相についての仕組みが書かれています。
Link to
hereトップレベル種注釈
KindSignatures拡張は、種の注釈を書けるようにするようなものでした。KindSignaturesは型パラメータの種を明示的に書くことができるようにする拡張でしたね。種が明示されないパラメータは、種推論によってその種が定まります。ですが、種推論は幾つか制約があり、その一つに再帰的データ型に対しては、単相的な再帰の種推論しか行えないというものがあります。以下のケースを見てください:
>>> :set -XPolyKinds
>>> data T m a = Nil | MkT (m a) (T Maybe (m a))
>>> :kind T
T :: (* -> *) -> * -> *このデータ型Tの種は(k -> *) -> k -> *というような多相化された種でも問題ないはずですが、実際にはPolyKindsをつけているにも関わらず*で単相化されて推論されます。単相制約によって、例えば次のように、一部種注釈を書いてもうまく推論できません:
>>> data T (m :: k -> *) a = Nil | MkT (m a) (T Maybe (m a))
<interactive>:49:45: error:
• Expected kind ‘k -> *’, but ‘Maybe’ has kind ‘* -> *’
• In the first argument of ‘T’, namely ‘Maybe’
In the type ‘T Maybe (m a)’
In the definition of data constructor ‘MkT’
>>> data T m (a :: k) = Nil | MkT (m a) (T Maybe (m a))
<interactive>:50:40: error:
• Expected kind ‘k -> *’, but ‘Maybe’ has kind ‘* -> *’
• In the first argument of ‘T’, namely ‘Maybe’
In the type ‘T Maybe (m a)’
In the definition of data constructor ‘MkT’ですが、私たちは完全に種推論に頼らないような種注釈を提供することで、T :: (k -> *) -> k -> *というような種多相化された型コンストラクタを作ることができます:
>>> data T (m :: k -> *) (a :: k) = Nil | MkT (m a) (T Maybe (m a))
>>> :kind T
T :: (k -> *) -> k -> *このような完全に種が提供されているような種注釈の形式を、GHCでは CUSKs(Complete User-Supplied Kind signatures) と呼んでいます。CUSKは、種多相な再帰的データ型を提供する場合必須のものになってきますが、上の例からも分かる通り非常に見にくいのが難点です。また構文を解析してCUSKか判断するのにも、手間がかかります。そのため、現在CUSKに代わるものとして、 トップレベル種注釈(top-level kind signatures) という機能が提案されています。この提案は、上の例のCUSKと同等の注釈を、次のように書けるようにするものです:
type T :: (k -> *) -> k -> *
data T m a = Nil | MkT (m a) (T Maybe (m a))関数の型注釈などと同じスタイルで、非常に見やすいですね。
トップレベル種注釈は、現在、GHC Proposals - Pull Request #54で提案されています。興味がある方は、GHC User’s Guide - 9.11.5 Complete user-supplied kind signatures and polymorphic recursionと合わせて提案内容を見てみると良いでしょう。
Link to
hereUnliftedデータ型
Haskellのデータ型は、liftedという枠組みの型でした。liftedな型は、評価されるまではサンクになっているのでした。unliftedな型は、GHCで幾つかプリミティブ型として提供されているのでした。現在、unliftedデータ型という拡張が提案されています。この拡張は、ユーザー定義のunliftedな型を定義できるようにする拡張です。
この拡張は、次のような新たなデータ宣言をできるようにするものです:
data unlifted UBool = UTrue | UFalseここで、UBool型の値は、unliftedな型でありボックス型であるようなデータ型になります。つまり、Array# aと同じようなデータ型で、サンクを持たずポインタでヒープ上の本体を指し示すような表現がされます。そして、その種はTYPE 'UnliftedRepになります。また、この拡張下では、unlifted型のnewtypeが行えるようにするという提案もされています。
ただこの拡張は新たなシンタックスを導入することになるため、GADTSyntaxとKindSignaturesを使って以下のようなことをできるようにすることが、代わりに提案されています:
{-# LANGUAGE GADTSyntax, KindSignatures #-}
data UBool :: TYPE 'UnliftedRep where
UTrue :: UBool
UFalse :: UBoolこれにより、新たな構文を導入しなくても、unliftedなデータ型を定義できるようになります。
unliftedデータ型について興味があるならば、GHC Wiki - UnliftedDataTypesのページを見てみると良いでしょう。このページに、主な提案内容が書かれています。
Link to
hereType in Type
TypeInType拡張は、DataKinds拡張とPolyKinds拡張をより強力にした拡張です。例えば、以下のようなことができるようになります:
>>> :set -XTypeInType -fprint-explicit-foralls
>>> -- 型エイリアスを種として使えるようになる
>>> type B = Bool
>>> data D (a :: B)
>>> :kind D
D :: B -> *
>>> -- より広い範囲の多相を書けるようになる
>>> data A (d :: D a)
>>> :kind A
A :: forall (a :: B). D a -> *
>>> -- RankN多相な種を書けるようになる
>>> :set -XRankNTypes
>>> data AN (d :: forall a. D a)
>>> :kind AN
AN :: (forall (a :: B). D a) -> *このように、型注釈でできたことが、種注釈でできるようになるわけです。
ただし、この拡張は現状とても不安定であり、使用が推奨されているわけではありません。この拡張を使用する場合は、コンパイル時、内部でこの拡張の挙動をチェックするように-dcore-lintというフラグを使用することが推奨されています。将来的には、この拡張の範囲を型と種の範囲から、型と値の範囲、ひいては種と型と値の違いを取り払い、依存型というシステムに徐々に近づけていくことも視野に入れているようです。ただし、まずは種と型の範囲で安定的な機能を提供するのが、目的ということでしょう。
TypeInType拡張については、主にGHC User’s Guide - 9.11.3 Overview of Type-in-Typeに、その概要が書かれています。
Link to
hereこの章のまとめ
この章では、幾つかの種に関する話題をかいつまんで紹介しました。
type roleは、二つの型が同じ内部表現を持つ型かを判定するための、型変数が持つ種とは異なる情報でした。nominal/representational/phantomの三種があり、データ宣言でどのtype roleを割り当てるかが推論されるのでした。また、RoleAnnotations拡張によって明示的に指定することも可能なのでした。
軽率多相(levity polymorphism)はlifted/unliftedの違いを吸収する多相でした。これによって、lifted/unliftedの違いを問わない多相化された関数を書けるようになるのでした。ただし、全ての関数を制限なく軽率多相化することはできず、関数の引数が軽率多相化されているようなものは、機械語にうまく翻訳できないため書けないのでした。
トップレベル種注釈は、既存のCUSKという種注釈の方法に変わり、種注釈を分かりやすく書くための提案でした。再帰的データ型に対して種推論がうまく働かないという制約から、多相的な種を使用する場合、種推論に頼らず完全な種の情報を提供する必要があり、完全に情報が提供されるような種の注釈をGHCではCUSKと読んでいるのでした。しかし、CUSKは一般的に見づらいため、それを解決するための提案でしたね。この提案されている構文は、関数の型注釈と同じスタイルで非常に分かりやすいですね。
unliftedデータ型は、unliftedな型を定義できるようにするような拡張として提案されているものでした。この拡張により、ボックス型でかつunliftedなもの、つまりサンクを持たないボックス型を定義できるようになるのでした。現状、幾つか議論されるべき課題が残っていますが、近い将来導入されるかもしれません。
TypeInTypeは型と種の違いを取り払うような拡張でした。これにより、型エイリアスを種に昇格したり、RankNの種注釈を書けるようになるのでした。ただし、現状は非常に不安定であり、使用には注意が必要です。
Link to
hereまとめ
さて、Part 1と合わせて、一通りの種に関する話題を紹介してきました。種の仕組みの紹介と5つの大きな話題を取り扱ってきました。また、少し高度な話題を幾つか、駆け足で紹介しました。この二つの記事が、何かの役に立てば幸いです。
もし、Advanced Topicsの内容について、詳細が知りたいという声が多ければ、Part 3を書くかもしれませんが、ひとまずはこれで。では、良いHaskellライフをノシ
Link to
here参考文献
- Haskell 2010 Language Report: Haskell2010の仕様書です。主に標準の仕組みを紹介する際に参照しました。
- 4.1 Overview of Types and Classes: 標準の型システムや型制約について、書かれています。
- GHC 8.2.1 Users Guide: 主な種に関する参考資料としてとGHC拡張についての資料として参考にしました。
- 9.2 Unboxed types and primitive operations: 非ボックス型を主とするプリミティブ型と、その演算のために用意されている関数についての解説が書かれています。
- 9.10 Datatype promotion:
DataKinds拡張の動機と解説が書かれています。 - 9.11 Kind polymorphism and Type-in-Type: GHCにおいての種推論などの、種に関することが総括してあります。
- 9.12 Levity polymorphism: 軽率多相に関するGHCでの主な仕組みや制約について解説されています。
- 9.14 Constraints in types: 型制約に関する、GHC上のいくつかの話題が書かれています。
- 9.36 Roles: type roleについての、動機と解説が書かれています。
- GHC Proposals: GHCでの実装面、言語面での提案を管理するリポジトリです。
- Revise Levity Polymorphism: GHC 8.2.1での軽率多相に関する変更が書かれています。
- Top-level kind signatures (instead of CUSKs): トップレベル型注釈に関しての提案です。
- GHC Developer Wiki: GHCの実装に関する事や、その元となるアイデアについてまとめられているWikiです。
- Commentary/Compiler/Kinds: この記事のストーリーを決める際に参照しました。
- Commentary/Compiler/TypeType: GHCの型にまつわる内部表現や分類法などについて書かれています。
- Commentary/Rts/Storage/HeapObjects: GHCオブジェクトの内部表現について書かれています。lifted/unlifted、boxed/unboxedの違いについて、参考にしました。
- GhcKinds:
PolyKinds拡張に関する話題がまとまっているページです。 - UnliftedDataTypes: unliftedデータ型を定義できるようにするための拡張の提案が、まとめられているページです。
- NoSubKinds: 軽率多相以前のGHCの仕組みとして、
OpenKindというものがありました。しかしながら、この仕組みは幾つか問題が知られており、現在は軽率多相によって置き換えられています。ここでは、OpenKindの仕組みと問題点、その解決法が書いてあります。
- その他の参考文献:
- Giving Haskell a Promotion:
DataKinds拡張の提唱論文です。DataKindsについて紹介する時、参考にしました。 - Levity Polymorphism (extended version): 軽率多相の提唱論文です。軽率多相について紹介する時、参考にしました。
- Unboxed values a non-strict as first class citizens in functional language: 非ボックス型の提唱論文です。unliftedな型の意味を紹介する場合に、参考にしました。
- Giving Haskell a Promotion:
型コンストラクタは値を持てないことに注意してください! 何らかの値を持つ型は全て
*という種を持つものになっており、例えばMaybe :: * -> *という型コンストラクタはそれだけでは値を持たず、Maybe Intなど型を一つ渡して初めて値を持つような型になるのでした。↩︎ここでの
Boolは、Bool型が種に昇格したものという点にも注意してくださいね!DataKinds拡張によって、データ型は種に昇格できるのでした。↩︎VecRepを持つプリミティブ型は紹介しませんでしたが、この型はSIMDベクトル演算を利用するために用意されています。VecCountはレーン数、VecElemはSIMD APIのどのデータ型を使用するかを表します。これらのプリミティブ型はSIMD Vectorsの章にまとまっているので、興味があれば見てみると良いでしょう。↩︎この種の定義は、GHC.Typesモジュールで確認することができます。他にも、エイリアスとして
TypeやUnicode版の★が用意されています。↩︎あなたがもし領域理論について興味があるならば、Domain Theoryを読んでみるのがよいでしょう。この文献は、領域理論に必要な順序理論の知識から、領域理論の基本的な概念を解説してくれている文献です。もし、理論自体に興味がなく、この理論がどのような問題解決を目指しているかだけを知りたいなら、Originsだけでも読むと良いでしょう。↩︎
非ボックス型は実データなので、サンクはどうやったって持てないんでしたね! 逆にliftedならば必ずポインタで表されているはずなので、ボックス型になります。ただし、unliftedだからといって非ボックス型とは限りません(例:
Array# a)。また、ボックス型だからといってliftedであるとは限りません。↩︎